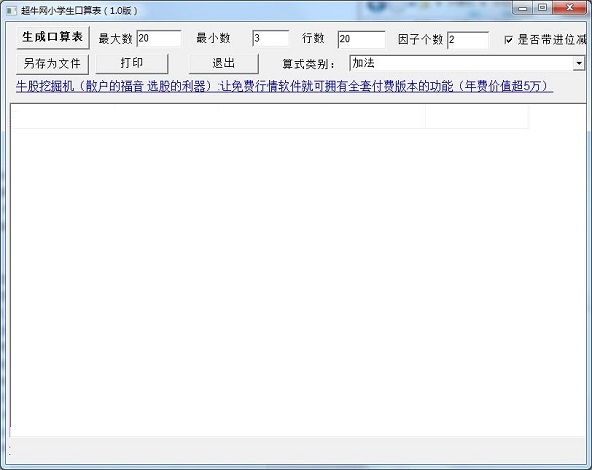
Features of automatic oral arithmetic generator for primary school students
1. Green and installation-free, just click to use
2. The oral arithmetic problem generator for primary school students supports customizing the maximum number, minimum number, number of rows, number of factors, etc.
3. Supports 7 algorithm types including addition, subtraction, multiplication and division.
4. The oral arithmetic problem generator for primary school students can help primary school students gradually improve their written arithmetic, oral arithmetic and mental arithmetic abilities.
Installation steps of automatic oral arithmetic generator for primary school students
1. Download the software package locally, unzip it, and run the "EXE. file"
2. Double-click to open

3. This software is green software and can be used without installation.
Steps to use the automatic oral arithmetic generator for primary school students
1. Open the oral arithmetic problem generator for primary school students, and first customize the generated maximum number, minimum number, number of rows and number of factors.

2. Complete these settings and click Generate Oral Arithmetic Bar to generate four arithmetic operations.
Four arithmetic rules for automatic generator of oral arithmetic for primary school students
1. In a calculation without parentheses, if there are only additions and subtractions or only multiplications and divisions, the calculations must be made from left to right, for example, 10.8-4.5+0.32=6.3+0.32=6.62
2. In a calculation without parentheses, if there are both multiplication and division as well as addition and subtraction, the multiplication and division must be calculated first, and then the addition and subtraction, for example, 10.8-4.5×0.32=10.8-1.44=9.36
3. In calculations with parentheses, calculate the values in the small brackets first, and then calculate the values in the square brackets. For example, (10.8-4.5)×0.32=6.3×0.32=2.016
4. Quick calculation of multiplication 1. Multiply two-digit numbers whose tens digit is 1
5. Multiply two-digit numbers whose ones digit is 1
6. Multiply two-digit numbers with the same tens and different ones
7. If the first digit is the same, the sum of the two mantissas is equal to 10 and multiplied by two digits.
8. The first digit is the same, and the mantissa is multiplied by a two-digit number not equal to 10.
9. The multiplicands are the same from beginning to end, and the sum of the beginning and end of the multiplier is 10 when multiplied by two digits.
10. The sum of the first and last numbers of the multiplicand is 10, and the multipliers are multiplied by two digits with the same first and last numbers.
11. The sum of the two first digits is 10. Multiply two digits with the same last digit.
Four arithmetic operations skills of the automatic generator for primary school students' oral arithmetic
1. Nature of moving
In an operation at the same level, a certain number can be moved to another position together with the operation symbol in front of it, and the result of the operation remains unchanged.
For example: a-b+c=a+c-b;a÷b×c=a×c÷b
2. Properties of bracket removal
In operations at the same level, if the parentheses are preceded by a plus sign or a multiplication sign, the operation symbols in the parentheses do not need to change signs when the parentheses are removed: if the parentheses are preceded by a minus sign or division sign, then when the parentheses are removed, the symbols in the parentheses will become its opposite symbol
For example: a+(b-c)=a+b-c
3. Nature of subtraction
If you subtract several numbers from a number continuously, you can use this number to subtract the sum of these numbers.
For example: a-b-c=a-(b+c)
4. Nature of division
If a number is divided by several numbers continuously, you can divide this number by the product of these numbers.
For example: a÷b÷c= a÷(b×c)
5. The property of constant quotient (neither b nor c is equal to 0)
a÷b= (a×c)÷ (b×c) a÷b= (a÷c)÷ (b÷c)
Simple calculation skills of four arithmetic operations with automatic oral arithmetic generator for primary school students
1. Rounding method
It is to use the laws of addition and multiplication and the properties of subtraction and division to round up calculations, that is, to round up a whole thousand, a whole hundred, or a whole number, and directly perform simple operations.
Example 1:3643-74+6357-126
=(3643+6357)-(74+126)
=1000-200
=800
By observing the characteristics of the numbers in the question, students are guided to use the operation laws of addition to add 3643 and 6357 to make a whole thousand, and to use the properties of subtraction to make 74 and 126 into a whole hundred, making the calculation simple
Example 2:125×25×4×8
=(125×8)×(25×4)
=1000×100
=100000
In this continuous multiplication formula, if you calculate from left to right as usual, it will be more troublesome and inflexible. If you apply the commutative law and associative law of multiplication, first calculate the product of 125 and 84, and get the whole thousand and the whole hundred. The number can make the calculation simple
Example 3:1400÷25÷4
=1400÷(25×4)
=1400÷100
=14
By observing the characteristics of the numbers in the question, students are guided to use the operation rules of continuous division. First, multiply 25 and 4 to make a hundred, and then divide the whole hundred by the dividend to make the calculation simple.
2. Tail removal method
During subtraction calculation, if the subtrahend and the minuend have the same mantissa, first subtract the subtrahend with the same mantissa from the minuend to make the calculation easier.
Example 1:2356-159-256
=2356-256-159
=2100-159
=1941
The second subtrahend 256 in the calculation formula has the same mantissa as the minuend 2356. You can exchange the positions of the two numbers and let 2356 be subtracted by 256 first, which can make the calculation simple.
3. Extract common factors method
Example 1:39×28+75×28-14×28
=(39+75-14)×28
=100×28
=2800
Guide students to observe the characteristics of the data and let them find that there is the same factor 28 in the three multiplication calculations, and the other three factors 39, 75, and 14 add and subtract them and the result is exactly 100. Then they can use the distributive law of multiplication in reverse to perform simple calculations.
4. Decomposition method
1. Decompose it into a "product"
According to the laws of operation and the characteristics of numbers, the numbers in calculation formulas are often decomposed and recombined flexibly to achieve rounding up and simple calculations.
Example 1:25×32×125
= 25×(4×8)×125
=(25×4)×(8×125)
=100×1000
=100000
This question decomposes the factor 32 in the continuous multiplication formula into the form of 4 × 8, and then multiplies 4 by 25 and 8 by 125 to get a formula for multiplying whole hundreds and whole thousands, which is relatively simple.
Example 2:8400÷140
=8400÷(7×20)
=8400÷7÷20
=1200÷20
=60
In this question, directly dividing 8400 by 140 cannot calculate the number quickly. If 140 is decomposed into 7×20, then first calculate 8400÷7 and then divide by 20, and the result will be easily calculated verbally.
2. Decompose into a "and"
It is to split a certain number in the operation into the sum of a whole thousand or a whole hundred, an integer plus a digit, to simplify the calculation
Example 1:105×36
=(100+5)×36
=100×36+5×36
=3600+180
=3780
In this question, it is easier to divide the factor 105, which is close to a hundred, into the sum of 100+5, and then use the distributive law of multiplication to calculate
3. Break it down into a “difference”
It is to convert a certain number in the operation into a whole thousand, a whole hundred, or a whole number minus one digit to simplify the calculation.
Example 1:548+99
=548+100-1
=648-1
=647
In this question, the addend 99, which is close to a hundred, is written in the form of 100-1. When calculating, it is easier to add the whole hundred first and then subtract one digit.
5. Expansion method
It is to use the product invariance rule and the quotient invariance property to expand or reduce the data in the calculation formula by the same multiple, thereby making the calculation simple. For some division problems, simple calculations can be performed based on the quotient invariance property.
Example 1:
8500÷25
=(8500×4)÷(25×4)
=34000÷100
=340
In this question, the quotient invariance law is used to expand the dividend 8500 and the divisor 25 by 4 times at the same time. The formula for dividing a whole hundred by multiple digits can be easily calculated verbally.
6. Transformation method
It is to transform the expression form of a certain data in the calculation formula to deform it, so as to use the laws of operation to simplify the calculation.
Example 1:
25×37+75×21
=25×37+(25×3)×21
=25×37+25×(3×21)
=25×37+25×63
=25×(37+63)
=25×100
=2500
This question does not seem to be simple on the surface, but after a little comparison and analysis of the numbers in the question, it can be seen that the factors 25 and 75 in the two multiplication equations are related. 75 is exactly 3 times of 25. First, 75×21 is rewritten into 25×3×21, and then into the form of 25×63. This produces a common factor of 25, and the distributive law of multiplication can be used for simple calculations.
Update log of automatic oral arithmetic generator for primary school students
1. Optimize content
2. The details are more outstanding and bugs are gone.
Huajun editor recommends:
After many updates and optimizations, the automatic oral arithmetic generator for primary school students has become more user-friendly and simpler to operate. The editor of Huajun Software Park personally tested it and recommends it to everyone. Interested friends can also download it.ACD ChemSketch,Jidao Junior High School Physics VR 3D Virtual Simulation Laboratory (Demo Version),GeoGebra 5.0.299.0,Gear parameter calculator,Enjoy Chemistry Assistant.







































it works
it works
it works