Introduction to permutations and combinations
Permutation and combination is the most basic concept of combinatorics. The so-called permutation means to sort a specified number of elements from a given number of elements. Combination refers to taking out only a specified number of elements from a given number of elements, regardless of sorting. The central problem of permutations and combinations is to study the total number of possible situations for permutations and combinations of given requirements. Permutation and combination are closely related to classical probability theory.
How to use the permutation and combination calculator
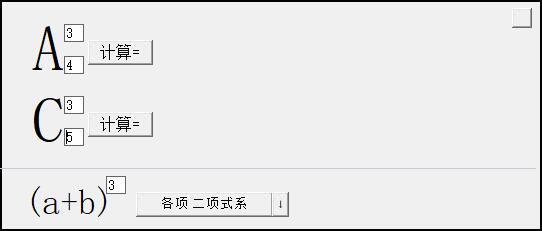
Arrange [Pnm (n is subscript, m is superscript)]
The factorial of number n: n! =n(n-1)(n-2)...2×1
Pnm=n×(n-1)....(n-m+1); Pnm=n! /(n-m)! (Note: ! is the factorial symbol); Pnn (the two n are superscript and subscript respectively) =n! ;0! =1;Pn1 (n is subscript 1 is superscript)=n
Combination [Cnm (n is subscript, m is superscript)]
Cnm=m(m-1)(m-2)...(m-n+1)/m! , Cnm=Pnm/Pmm; Cnm=n! /m! (n-m)! ;Cnn (two n are superscript and subscript respectively) =1; Cn1 (n is subscript and 1 is superscript)=n; Cnm=Cn (n-m)



































Useful
Useful
Useful